Mean Street Gallery - Exploring Data Averages

15 Jul, 2025

Have you ever felt a little lost when numbers start flying around, especially when people talk about averages or what's typical? It's something that happens to many of us, really. We often hear about the "average" of this or the "middle" of that, but what do those words actually mean for the information we see every single day? It can feel a bit like walking down a busy street, full of signs and sounds, trying to make sense of it all.

Well, just like you might visit a place to see a collection of interesting things, we are going to take a peek at a kind of "mean street gallery" where numbers hang out. This gallery, in a way, shows us how to look at collections of facts and figures and pull out the core ideas. It's about finding the pulse of a group of numbers, giving us a clearer picture without getting lost in every single detail. It’s a bit like finding the main theme in a long story, so to speak.

Luckily, there are some pretty cool resources out there that help make this kind of numerical exploration much less intimidating. Think of it as having a friendly guide for your visit to this conceptual gallery. Places like Khan Academy, for instance, are really good at breaking down these ideas into easy-to-follow steps, making it so much simpler to grasp what these statistical tools are all about. They help you get a sense of what the numbers are trying to tell you, which is very helpful.

What is the "Mean" on Our Data Street?
- The Core Idea of a Data Collection
How Do We Find the Average in the Mean Street Gallery?
- Getting to Grips with Calculations
Beyond the Average- What Else Lives on This Street?
- The Middle Ground- Our Median Street View
- The Most Common Sight- The Mode
Why Do These Numbers Matter for Your Mean Street Gallery?
- Making Sense of the Information Around Us
A Closer Look at Data Spread
- Understanding Variation on the Mean Street
Is There a Right Way to Summarize Data?
- Picking the Best Tool for the Job
Learning from the Experts at Khan Academy
- Free Resources for Your Data Curiosity
The Future of Learning and Our Mean Street Gallery
- Exploring New Ways to Grasp Data

What is the "Mean" on Our Data Street?

When we talk about the "mean," we are, in a way, talking about the average value within a collection of numerical pieces of information. It's a way to get a single number that gives us a quick idea of what the whole group of numbers looks like. Think of it as finding the central point, or the typical value, for a bunch of different measurements. This idea of the mean is used to give a short picture of a data collection, so to speak. It’s a way to measure where the center of a group of numbers might be, which is really quite useful.

For instance, if you have a group of heights from different people, the mean height would be that single number that represents the average height of everyone in that group. It helps us summarize things rather quickly. The mean helps us get a sense of the middle, or the very center, of the numerical facts we are looking at. It’s a pretty fundamental concept in statistics, and it helps us make sense of various kinds of information, you know, from everyday observations to scientific studies.

The Core Idea of a Data Collection

A data collection is simply a group of numbers or observations that we have gathered. It could be anything from the scores on a test to the number of cars passing a certain point in an hour. When we are looking at a collection like this, the mean is one of the main tools we use to get a quick summary. It helps us to see the overall trend or the typical value within that particular set of figures. It’s almost like getting a snapshot of the entire group, giving us a general idea without having to look at every single number individually, which is pretty handy.

This is where Khan Academy comes in, offering a rather comprehensive review of these basic concepts in statistics. They help people learn about the mean, along with the median and mode, by walking through some basic examples. This makes it easier to practice with problems, which is quite helpful for getting a solid grasp of these ideas. So, if you are ever wondering what a collection of numbers is trying to tell you, the mean is often the first place to look, honestly.

How Do We Find the Average in the Mean Street Gallery?

Finding the mean, or the average, of a collection of numbers is a pretty straightforward process. It involves two simple steps. First, you take all the numbers in your group and add them up. You just gather them all together, so to speak, and combine their values. Then, once you have that total sum, you simply divide it by the total count of how many numbers you had in your original group. That result is your mean. It's a method that is quite simple, but it gives us a very powerful piece of information about the entire collection of numbers. It’s a basic arithmetic process that yields a lot of insight, really.

For instance, if you had the numbers 2, 4, and 6, you would add them up to get 12. Since there are three numbers in that group, you would then divide 12 by 3, which gives you 4. So, the mean of 2, 4, and 6 is 4. It’s a pretty clear way to find the middle ground. This kind of calculation is something you can practice with, and there are many opportunities to try problems that help you get comfortable with it. It’s your first opportunity to practice with us, as a matter of fact, when you start looking at these ideas.

Getting to Grips with Calculations

Learning how to figure out the mean by going through some basic examples and trying out practice problems is a really effective way to get comfortable with this idea. It helps you see how the numbers work together and what the resulting average truly represents. The process itself is not overly complicated, but doing it a few times helps solidify the understanding. You are basically taking all the individual pieces of information and finding one representative number for the whole group. This is a skill that is quite useful in many different areas, from understanding sports scores to looking at financial reports, you know.

Khan Academy provides specific exercises where they give you a group of numbers and then ask you to find the mean, median, and mode. This kind of hands-on practice is really important for getting a feel for these concepts. It’s your first chance to put what you've learned into action, and it helps you build confidence in your ability to work with numerical facts. So, practicing these calculations is a key part of truly grasping what the mean represents and how it helps us understand collections of numbers, which is pretty cool.

Beyond the Average- What Else Lives on This Street?

While the mean gives us a good sense of the average, it's not the only way to look at the center of a group of numbers. There are other important measures that live on this "data street" that can give us different perspectives. Sometimes, the mean might not tell the whole story, especially if there are some numbers that are much, much larger or smaller than the rest. That’s when we might turn to other tools, which is quite interesting. These other measures help us get a more complete picture of what’s going on within a collection of numbers, offering different ways to pinpoint the "middle" or the "typical" value, as a matter of fact.

The Middle Ground- Our Median Street View

Imagine lining up all the numbers in your collection from the smallest to the largest. The median is simply the number that sits right in the very middle of that ordered list. If you have an odd number of values, it's the one right there in the center. If you have an even number of values, you take the two middle ones, add them together, and then divide by two to find your median. It's a way to find the true middle point, unaffected by unusually high or low numbers. The median is the middle value when a data set is ordered from, you know, smallest to largest. It gives us a different kind of center, one that is not pulled around by extreme values, which is quite useful in certain situations.

The Most Common Sight- The Mode

The mode is perhaps the easiest of these measures to grasp. It's simply the number that appears most often in your collection of numbers. If a certain number shows up more frequently than any other, then that's your mode. A group of numbers can have one mode, many modes, or no mode at all if every number appears only once. It tells you which value is the most common or popular within your group. It’s a straightforward way to see what value pops up the most, which can be very informative, especially when you are looking at things like preferences or common occurrences, for example.

Why Do These Numbers Matter for Your Mean Street Gallery?

These measures—mean, median, and mode—are not just abstract concepts for school. They are tools that help us make sense of the numerical information that surrounds us every single day. They help us summarize collections of numbers with a single representative number, making it easier to understand what's going on without getting bogged down in every individual detail. Whether you are looking at average temperatures, typical incomes, or the most common shoe size, these ideas are always at play. They help us draw quick conclusions and make comparisons, which is pretty essential for understanding the world, really.

For example, if you hear about a study that measured people's blood pressure, you might be told the average blood pressure for the group. The provided text mentions a large sample of females had their systolic blood pressure measured, and the mean blood pressure was 125 millimeters of mercury, with a standard deviation of 10 millimeters of mercury. This single number, the mean, gives you a quick summary of what was typical for that group. Without it, you would have to look at hundreds or thousands of individual blood pressure readings, which would be quite overwhelming. So, these numbers truly help us condense large amounts of information into something manageable, which is very helpful.

Making Sense of the Information Around Us

These statistical ideas help us simplify and interpret collections of numbers. They give us a way to describe the "center" of a group of numbers, helping us to grasp the overall picture without getting lost in the individual pieces. It's about finding that key piece of information that tells us a lot about the whole group. For instance, knowing the average test score for a class tells you a lot more than just knowing everyone's individual score, especially if you want a quick overview. It’s a way of making sense of the world, in a way, by finding the typical or central value in various situations.

The ability to calculate and interpret these measures is a fundamental skill for anyone dealing with numerical information. It allows you to move beyond just seeing numbers to actually understanding what they represent and what they are trying to communicate. This kind of understanding is useful in so many different areas, from science and business to just making informed decisions in your personal life. It’s about gaining clarity from what might otherwise seem like a jumble of figures, you know.

A Closer Look at Data Spread

While the mean, median, and mode tell us about the center of a collection of numbers, it's also really helpful to know how spread out those numbers are. Are they all clustered closely around the average, or are they scattered far apart? This idea of spread or variation is also a very important aspect of understanding a collection of numbers. It gives us a sense of how consistent or how varied the numbers are within a given group. It’s a bit like knowing not just the average height of people on a street, but also if everyone is nearly the same height or if there are very short and very tall people, too.

Understanding Variation on the Mean Street

The text mentions "standard deviation," which is a way to measure how much the numbers in a group typically differ from the mean. A small standard deviation means the numbers are generally close to the average, while a large standard deviation means they are more spread out. For example, in the blood pressure example, a standard deviation of 10 millimeters of mercury tells us something about how much individual blood pressure readings typically varied from that average of 125. It helps us understand the typical distance of each data point from the average, which is pretty useful.

Another related concept is the mean absolute deviation (MAD). This is another way to look at how much, on average, each number in a collection differs from the mean. It helps you get a sense of the typical distance between each number and the average value. Learning to practice finding the mean absolute deviation of a data set helps you grasp this idea of spread. It’s about understanding not just where the center is, but also how much the numbers tend to wander away from that center, which is very insightful.

Is There a Right Way to Summarize Data?

When you are looking at a collection of numbers, you might wonder if there is one "best" way to summarize them. The truth is, it really depends on what you are trying to understand and what kind of numbers you have. Sometimes the mean is the most appropriate measure, but other times the median or even the mode might give you a better picture. It’s about choosing the tool that fits the situation best, as a matter of fact. There isn't a single answer that works for every scenario, which is something to keep in mind, you know.

Picking the Best Tool for the Job

For example, if you have a group of incomes, and there are a few people who earn an extremely large amount, the mean income might be pulled up by those high earners, making it seem like everyone earns more than they actually do. In that case, the median income, which is the middle value, might give you a more realistic idea of what a typical person earns. It's about being smart with your choice of summary. Each measure offers a unique perspective, and understanding when to use each one is a key part of working with numerical information. It's about getting the most honest picture from your numbers, honestly.

Learning from the Experts at Khan Academy

When it comes to learning about these kinds of numerical ideas, resources like Khan Academy are truly fantastic. They offer free learning materials on a huge range of subjects, including math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, and history, among others. Their approach makes complex topics accessible to just about anyone. They provide clear explanations and lots of opportunities to practice what you are learning, which is incredibly helpful for building confidence and a solid understanding. It’s almost like having a personal tutor available whenever you need one, which is really quite amazing.

Free Resources for Your Data Curiosity

Khan Academy is a nonprofit organization with the mission of providing a free, world-class education for anyone, anywhere. This means they are dedicated to making knowledge available to everyone, without cost. This commitment extends to exploring what new technologies, like artificial intelligence, could mean for the future of education. They are always looking for ways to improve how people learn and understand important concepts. So, if you have a curiosity about numbers, or any other subject for that matter, their resources are a great place to start. They make learning feel approachable and even fun, which is very important.

The lessons are often created by people like Sal Khan and the Monterey Institute for Technology, ensuring that the content is well-explained and accurate. They break down complex topics into smaller, digestible pieces, making it easier to grasp even the most challenging ideas. It’s your first opportunity to practice with them, and they offer a supportive environment for learning at your own pace. This kind of access to high-quality educational material is a real benefit for anyone looking to build their knowledge and skills, honestly.

The Future of Learning and Our Mean Street Gallery

As a nonprofit educational organization, Khan Academy sees it as their responsibility to explore what new technologies could mean for the future of education. This means they are constantly thinking about how to make learning even more effective and accessible for everyone. Imagine how these tools could help us better explore our "mean street gallery" of data, making it even easier to grasp the meaning behind the numbers we encounter. It’s a very forward-thinking approach to education, aiming to prepare learners for whatever the future might hold, which is quite inspiring.

Exploring New Ways to Grasp Data

The continuous exploration of new teaching methods and technologies means that understanding concepts like mean, median, and mode will only become more intuitive and engaging. They are always working to refine how they present information, ensuring that learners can truly connect with the material. This commitment to innovation helps people not just memorize facts, but truly understand the underlying principles. It’s about building a solid foundation of knowledge that can be applied in many different situations, which is very valuable. So, the journey to understanding data, whether it's through simple averages or more complex measures, is constantly being made clearer and more approachable, which is pretty neat.

Details

Details

Mean vs. Average: Confusing Math and Statistics Terms • 7ESL

Details

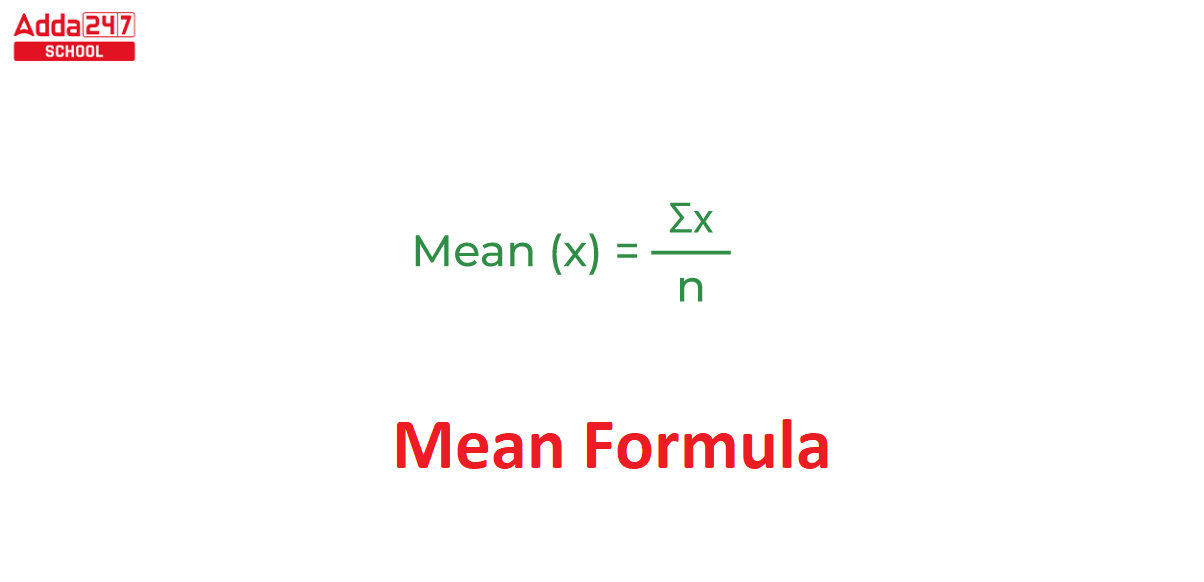
Detail Author:

Name : Vella Veum
Username : robel.madisyn
Email : gracie.schaden@yahoo.com
Birthdate : 1977-05-11
Address : 12687 Alexandrine Spur North Estevan, DE 25989-7399
Phone : 717-967-0119
Company : Weimann-Rempel
Job : Librarian
Bio : Ut maxime dolor minima molestias dignissimos maiores. Veniam harum aliquid excepturi et autem. Et et error doloribus sint. Amet pariatur sit molestiae ea sint.

Socials

instagram:

url : https://instagram.com/stiedemann1985
username : stiedemann1985
bio : Ut et voluptas culpa et veritatis aut nobis. Ad quos amet enim dignissimos pariatur.
followers : 6913
following : 1686